1. definīcija. Skaitļa ass ( skaitļa līnija, koordinātu līnija) Ox ir taisne, uz kuras ir izvēlēts punkts O izcelsme (koordinātu izcelsme)(1. att.), virziens
O → x
uzskaitīti kā pozitīvs virziens un tiek atzīmēts segments, kura garums tiek pieņemts garuma vienība.


2. definīcija. Segmentu, kura garums tiek ņemts par garuma vienību, sauc par skalu.
Katram skaitļu ass punktam ir koordinātas, kas ir reāls skaitlis. Punkta O koordināta ir nulle. Patvaļīga punkta A koordināte, kas atrodas uz stara Ox, ir vienāda ar segmenta OA garumu. Skaitliskās ass patvaļīga punkta A koordināte, kas neatrodas uz stara Ox, ir negatīva un absolūtā vērtībā ir vienāda ar segmenta OA garumu.
3. definīcija. Taisnstūra Dekarta koordinātu sistēma Oxy uz plaknes zvaniet diviem savstarpēji perpendikulāri ciparu asis Ox un Oy ar tāds pats mērogs Un kopīgs atskaites punkts punktā O un tā, lai rotācija no stara Ox 90° leņķī pret staru Oy tiktu veikta virzienā pretpulksteņrādītājvirzienā(2. att.).


Piezīme. Tiek saukta taisnstūra Dekarta koordinātu sistēma Oxy, kas parādīta 2. attēlā pareizā sistēma koordinātas, Atšķirībā no kreisās koordinātu sistēmas, kurā tiek veikta sijas Ox rotācija 90° leņķī pret siju Oy pulksteņrādītāja kustības virzienā. Šajā rokasgrāmatā mēs mēs uzskatām tikai labās puses koordinātu sistēmas, to īpaši nenorādot.
Ja plaknē ieviešam kādu taisnstūra Dekarta koordinātu sistēmu Oxy, tad katrs plaknes punkts iegūs divas koordinātas – abscisa Un ordinātas, kuras aprēķina šādi. Lai A ir patvaļīgs punkts plaknē. Nometīsim perpendikulus no punkta A A.A. 1 un A.A. 2 uz taisnēm attiecīgi Ox un Oy (3. att.).


4. definīcija. Punkta A abscise ir punkta koordināte A 1 uz skaitļa ass Ox, punkta A ordināta ir punkta koordināte A 2 uz skaitļu ass Oy.
Apzīmējums Punkta koordinātas (abscisa un ordināta). A taisnstūra Dekarta koordinātu sistēmā Oxy (4. att.) parasti apzīmē A(x;y) vai A = (x; y).
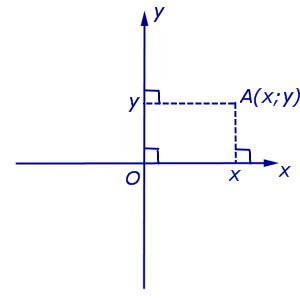

Piezīme. Punkts O, saukts izcelsmi, ir koordinātas O(0 ; 0) .
5. definīcija. Taisnstūra Dekarta koordinātu sistēmā Oxy skaitlisko asi Ox sauc par abscisu asi, bet skaitlisko asi Oy par ordinātu asi (5. att.).
6. definīcija. Katra taisnstūra Dekarta koordinātu sistēma plakni sadala 4 ceturtdaļās (kvadrantos), kuru numerācija parādīta 5. attēlā.


7. definīcija. Tiek izsaukta plakne, uz kuras ir dota taisnstūra Dekarta koordinātu sistēma koordinātu plakne.
Piezīme. Abscisu asi koordinātu plaknē norāda vienādojums y= 0, ordinātu ass ir norādīta koordinātu plaknē ar vienādojumu x = 0.
1. paziņojums. Attālums starp diviem punktiem koordinātu plakne
A 1 (x 1 ;y 1) Un A 2 (x 2 ;y 2)
aprēķināts saskaņā ar formulu
Pierādījums . Apsveriet 6. attēlu.


Veidošanas funkcija
Jūsu uzmanībai piedāvājam funkciju grafiku konstruēšanas pakalpojumu tiešsaistē, uz kuru visas tiesības pieder uzņēmumam Desmos. Izmantojiet kreiso kolonnu, lai ievadītu funkcijas. Varat ievadīt manuāli vai izmantojot virtuālo tastatūru loga apakšā. Lai palielinātu logu ar grafiku, varat paslēpt gan kreiso kolonnu, gan virtuālo tastatūru.
Tiešsaistes diagrammu veidošanas priekšrocības
- Vizuāls ievadīto funkciju displejs
- Ļoti sarežģītu grafiku veidošana
- Netieši norādīto grafiku konstruēšana (piemēram, elipse x^2/9+y^2/16=1)
- Iespēja saglabāt diagrammas un saņemt saiti uz tām, kas kļūst pieejama ikvienam internetā
- Mēroga kontrole, līniju krāsa
- Iespēja attēlot grafikus pa punktiem, izmantojot konstantes
- Vairāku funkciju grafiku zīmēšana vienlaikus
- Uzzīmējiet polāros koordinātos (izmantojiet r un θ(\theta))
Ar mums tiešsaistē ir viegli izveidot dažādas sarežģītības diagrammas. Būvniecība tiek veikta uzreiz. Pakalpojums ir pieprasīts funkciju krustpunktu atrašanai, grafiku attēlošanai tālākai to pārvietošanai Word dokumentā kā ilustrācijas uzdevumu risināšanā, funkciju grafiku uzvedības pazīmju analīzei. Optimālais pārlūks darbam ar diagrammām šajā vietnes lapā ir Google Chrome. Pareiza darbība netiek garantēta, izmantojot citas pārlūkprogrammas.
Apkārtmērs ir plaknes punktu kopa, kas atrodas vienādā attālumā no dotā punkta, ko sauc par centru.
Ja punkts C ir apļa centrs, R ir tā rādiuss un M ir patvaļīgs apļa punkts, tad pēc apļa definīcijas
Vienlīdzība (1) ir apļa vienādojums rādiuss R ar centru punktā C.
Pieņemsim taisnstūra Dekarta koordinātu sistēmu (104. att.) un punktu C( A; b) ir apļa centrs ar rādiusu R. Ļaujiet M( X; plkst) ir patvaļīgs šī apļa punkts.
Kopš |SM| = \(\sqrt((x - a)^2 + (y - b)^2) \), tad vienādojumu (1) var uzrakstīt šādi:
\(\sqrt((x - a)^2 + (y - b)^2) \) = R
(x-a) 2 + (y - b) 2 = R 2 (2)
Vienādojumu (2) sauc vispārējs apļa vienādojums vai vienādojums aplim ar rādiusu R ar centru punktā ( A; b). Piemēram, vienādojums
(x - l) 2 + ( y + 3) 2 = 25
ir vienādojums aplim ar rādiusu R = 5 ar centru punktā (1; -3).
Ja apļa centrs sakrīt ar koordinātu sākumpunktu, tad vienādojums (2) iegūst formu
x 2 + plkst 2 = R2. (3)
Vienādojumu (3) sauc apļa kanoniskais vienādojums .
1. uzdevums. Uzrakstiet vienādojumu aplim, kura rādiuss ir R = 7 un kura centrs atrodas sākuma punktā.
Tieši aizvietojot rādiusa vērtību vienādojumā (3), mēs iegūstam
x 2 + plkst 2 = 49.
2. uzdevums. Uzrakstiet vienādojumu aplim ar rādiusu R = 9 ar centru C(3; -6).
Formulā (2) aizstājot punkta C koordinātu vērtību un rādiusa vērtību, iegūstam
(X - 3) 2 + (plkst- (-6)) 2 = 81 vai ( X - 3) 2 + (plkst + 6) 2 = 81.
3. uzdevums. Atrodiet apļa centru un rādiusu
(X + 3) 2 + (plkst-5) 2 =100.
Salīdzinot šo vienādojumu ar vispārējo apļa vienādojumu (2), mēs to redzam A = -3, b= 5, R = 10. Tāpēc C(-3; 5), R = 10.
4. uzdevums. Pierādiet, ka vienādojums
x 2 + plkst 2 + 4X - 2y - 4 = 0
ir apļa vienādojums. Atrodiet tā centru un rādiusu.
Pārveidosim šī vienādojuma kreiso pusi:
x 2 + 4X + 4- 4 + plkst 2 - 2plkst +1-1-4 = 0
(X + 2) 2 + (plkst - 1) 2 = 9.
Šis vienādojums ir apļa vienādojums, kura centrs ir (-2; 1); Apļa rādiuss ir 3.
5. uzdevums. Uzrakstiet vienādojumu riņķim ar centru punktā C(-1; -1), kas pieskaras taisnei AB, ja A (2; -1), B(- 1; 3).
Uzrakstīsim līnijas AB vienādojumu:
![]() vai 4 X + 3y-5 = 0.
vai 4 X + 3y-5 = 0.
Tā kā aplis pieskaras noteiktai līnijai, saskares punktam novilktais rādiuss ir perpendikulārs šai līnijai. Lai atrastu rādiusu, jums jāatrod attālums no punkta C(-1; -1) - apļa centra līdz taisnei 4 X + 3y-5 = 0:
Uzrakstīsim vēlamā apļa vienādojumu
(x +1) 2 + (y +1) 2 = 144 / 25
Dots aplis taisnstūra koordinātu sistēmā x 2 + plkst 2 = R2. Apsveriet tā patvaļīgo punktu M( X; plkst) (105. att.).

Ļaujiet rādiusa vektoram OM> punkts M veido lieluma leņķi t ar pozitīvu O ass virzienu X, tad punkta M abscises un ordinātas mainās atkarībā no t
(0 t x un y cauri t, mēs atradām
x= Rcos t ; y= R grēks t , 0 t
Vienādojumus (4) sauc apļa parametriskie vienādojumi ar centru sākuma punktā.
6. uzdevums. Aplis tiek dots ar vienādojumiem
x= \(\sqrt(3)\)cos t, y= \(\sqrt(3)\)sin t, 0 t
Pierakstiet šī apļa kanonisko vienādojumu.
Tas izriet no nosacījuma x 2 = 3, jo 2 t, plkst 2 = 3 grēks 2 t. Saskaitot šīs vienādības pēc termiņa, mēs iegūstam
x 2 + plkst 2 = 3 (cos 2 t+ grēks 2 t)
vai x 2 + plkst 2 = 3
Nodarbības mērķis: iepazīstināt ar riņķa vienādojumu, iemācīt skolēniem sastādīt apļa vienādojumu, izmantojot gatavu zīmējumu, un konstruēt apli, izmantojot doto vienādojumu.
Aprīkojums: interaktīvā tāfele.
Nodarbības plāns:
- Organizatoriskais brīdis – 3 min.
- Atkārtojums. Garīgās darbības organizēšana – 7 min.
- Jaunā materiāla skaidrojums. Apļa vienādojuma atvasināšana – 10 min.
- Apgūstamā materiāla konsolidācija – 20 min.
- Nodarbības kopsavilkums – 5 min.
Nodarbību laikā
2. Atkārtošana:
− (1.pielikums 2. slaids) pierakstiet nogriežņa vidus koordinātu atrašanas formulu;
− (3. slaids) Z Uzrakstiet formulu attālumam starp punktiem (nozares garumu).
3. Jaunā materiāla skaidrojums.
(4.–6. slaids) Definējiet apļa vienādojumu. Atvasiniet apļa vienādojumus ar centru punktā ( A;b) un centrēts uz izcelsmi.
(X – A ) 2 + (plkst – b ) 2 = R 2 – apļa ar centru vienādojums AR (A;b) , rādiuss R , X Un plkst – patvaļīga apļa punkta koordinātas .
X 2 + y 2 = R 2 – apļa vienādojums ar centru sākuma punktā.
(7. slaids)
Lai izveidotu apļa vienādojumu, jums ir nepieciešams:
- zināt centra koordinātas;
- zināt rādiusa garumu;
- Apļa vienādojumā aizstājiet centra koordinātas un rādiusa garumu.
4. Problēmu risināšana.
Uzdevumos Nr.1 – Nr.6 sastādiet riņķa vienādojumus, izmantojot gatavus rasējumus.



(14. slaids)
№ 7. Aizpildiet tabulu.

(15. slaids)
№ 8. Izveidojiet apļus savā piezīmju grāmatiņā, izmantojot vienādojumus:
A) ( X – 5) 2 + (plkst + 3) 2 = 36;
b) (X + 1) 2 + (plkst– 7) 2 = 7 2 .
(16. slaids)
№ 9. Atrodiet centra koordinātas un rādiusa garumu, ja AB- apļa diametrs.
| Ņemot vērā: | Risinājums: | ||
| R | Centra koordinātas | ||
| 1 | A(0 ; -6) IN(0 ; 2) |
AB 2 = (0 – 0) 2 + (2 + 6) 2 ; AB 2 = 64; AB = 8 . |
A(0; -6) IN(0 ; 2) AR(0 ; – 2) – centrs |
| 2 | A(-2 ; 0) IN(4 ; 0) |
AB 2 = (4 + 2) 2 + (0 + 0) 2 ; AB 2 = 36; AB = 6. |
A (-2;0) IN (4 ;0) AR(1 ; 0) – centrs |
(17. slaids)
№ 10. Uzrakstiet vienādojumu aplim, kura centrs atrodas sākuma punktā un iet caur punktu UZ(-12;5).
Risinājums.
R 2 = Labi 2
= (0 + 12) 2 +
(0 – 5) 2 = 144 + 25 = 169;
R= 13;
Apļa vienādojums: x 2 + y 2 = 169 .
(18. slaids)
№ 11. Uzrakstiet vienādojumu aplim, kas iet caur sākuma punktu un kura centrs ir AR(3; - 1).
Risinājums.
R2= OS 2 = (3 – 0) 2 + (–1–0) 2 = 9 + 1 = 10;
Apļa vienādojums: ( X - 3) 2 + (y + 1) 2 = 10.
(19. slaids)
№ 12. Uzrakstiet vienādojumu aplim ar tā centru A(3;2), kas iet cauri IN(7;5).
Risinājums.
1. Apļa centrs – A(3;2);
2.R = AB;
AB 2 = (7 – 3) 2 + (5 – 2) 2 = 25; AB
= 5;
3. Apļa vienādojums ( X – 3) 2 + (plkst − 2) 2
= 25.
(20. slaids)
№ 13. Pārbaudiet, vai punkti atrodas A(1; -1), IN(0;8), AR(-3; -1) uz apļa, kas definēts ar vienādojumu ( X + 3) 2 + (plkst − 4) 2 = 25.
Risinājums.
es. Aizstāsim punkta koordinātas A(1; -1) apļa vienādojumā:
(1 + 3) 2 +
(−1 − 4) 2 =
25;
4 2 + (−5) 2 = 25;
16 + 25 = 25;
41 = 25 – vienlīdzība ir nepatiesa, kas nozīmē A(1; -1) nemelo uz apļa, kas dots ar vienādojumu ( X + 3) 2 +
(plkst −
4) 2 =
25.
II. Aizstāsim punkta koordinātas IN(0;8) apļa vienādojumā:
(0 + 3) 2 +
(8 − 4) 2 =
25;
3 2 + 4 2 = 25;
9 + 16 = 25;
IN(0;8)meli X + 3) 2 +
(plkst − 4) 2
=
25.
III. Aizstāsim punkta koordinātas AR(-3; -1) apļa vienādojumā:
(−3 + 3) 2 +
(−1− 4) 2 =
25;
0 2 + (−5) 2 = 25;
25 = 25 – vienlīdzība ir patiesa, kas nozīmē AR(-3; -1) meli uz apļa, kas dots ar vienādojumu ( X + 3) 2 +
(plkst − 4) 2
=
25.
Nodarbības kopsavilkums.
- Atkārtojiet: apļa vienādojums, apļa vienādojums ar tā centru sākuma punktā.
- (21. slaids) Mājasdarbs.